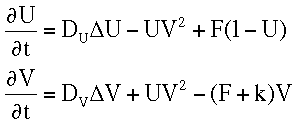-- CENTRAL STATION --
A collection of references on
High-Resolution Non-Oscillatory Central Schemes
Second-order central schemes in one-space dimensionThird-and higher-order central schemes in one-space dimensionNon oscillatory central schemes in several space dimensionsNon oscillatory central schemes on unstructured and overlapping gridsNon oscillatory central schemes for incompressible flowsNon oscillatory central schemes for Hamilton-Jacobi equationsApplications of non-oscillatory central schemes for semi-conductorsApplications to Sedimentation, Flocculations and related modelsNon oscillatory central schemes -- applications to...
Multi-component problemsRelaxation problems and stiff source termsExtended thermodynamicsBalance laws: Shallow-water/Saint-Venant, Solar atmosphere, ...
Saturating dissipationHomogenization and multiscaleDiscrete kinetic modelsMHDThe p-systemRiemann problemsGranular AvalanchesSecond order central schemes in one space dimension
Back to TopH. Nessyahu & E. Tadmor (1990) [
pdf file]Non-oscillatory central differencing for hyperbolic conservation lawsJournal of Computational Physics 87 (1990) 408-463.
D. Levy & E. Tadmor (1997) [
postscript file]Non-oscillatory boundary treatment for staggered central schemes
G.-S. Jiang, D. Levy, C.-T. Lin, S. Osher & E. Tadmor (1998) [
pdf file]High-resolution non-oscillatory central schemes with non-staggered grids for hyperbolic conservation lawsSIAM Journal on Numerical Analysis 35 (1998) 2147-2168.
A. Kurganov & E. Tadmor (2000) [
pdf file]New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equationsJournal of Computational Physics 160 (2000) 214-282.
A. Kurganov & G. Petrova (2000) [
pdf file]Central schemes and contact discontinuitiesMathematical Modelling and Numerical Analysis 34 (2000) 1259-1275.
K.-A. Lie & S. Noelle (2003) [
pdf file]On the artificial compression method for second-order nonoscillatory central difference schemes for systems of conservation lawsSIAM J. Scientific Computation 24 (2003) 1157-1174.
Third and higher order central schemes in one space dimension
Back to TopX-D. Liu & E. Tadmor (1998) [
pdf file]Third order nonoscillatory central scheme for hyperbolic conservation lawsNumerische Mathematik 79 (1998) 397-425.
F. Bianco, G. Puppo & G. Russo (1998) [
pdf file]High order central schemes for hyperblic systems of conservation laws"Hyperbolic Problems: Theory, Numerics, Applications", Proceedings of the 7th international conference held in Zurich, Feb. 1998 (M. Fey and R. Jeltsch, eds.), Int'l series in Numer. Math. Vol 129, Birkhauser, 1999, 55-64.
F. Bianco, G. Puppo & G. Russo (1999) [
pdf file]High order central schemes for hyperbolic systems of conservation lawsSIAM Journal on Scientific Computing 21 (1999) 294-322.
D. Levy, G. Puppo & G. Russo (1999) [
pdf file]Central WENO schemes for hyperbolic systems of conservation lawsMathematical Modelling and Numerical Analysis 33 (1999) 547-571.
D. Levy, G. Puppo & G. Russo (2000) [
pdf file]On the behavior of the total variation in CWENO methods for conservation lawsApplied Numerical Mathematics 33 (2000) 407-414.
A. Kurganov & D. Levy (2000) [
pdf file]A third-order semi-discrete central scheme for conservation laws and convection-diffusion equationSIAM Journal on Scientific Computing 22 (2000) 1461-1488.
G. Puppo (2002) [
pdf file]Numerical entropy production on shocks and smooth transitionsJournal of Scientific Computing 17 (2002) 263-271.
J. Qiu & C.-W. Shu (2002) [
pdf file]On the construction, comparison, and local characteristic decompositions for high order central WENO schemesJournal of Computational Physics 183 (2002) 187-209.
E. Tadmor & J. Tanner (2003) [
pdf file]An adaptive order Godunov type central scheme"Hyperbolic Problems: Theory, Numerics, Applications", Proceedings of the 9th international conference held in CalTech, Mar. 2002, (T. Hou & E. Tadmor eds.) Springer 2003, pp. 871-880.
Central schemes in several space dimensions
Back to TopG.-S. Jiang & E. Tadmor (1998) [
pdf file]Non-oscillatory central schemes for multidimensional hyperbolic conservation lawsSIAM Journal on Scientific Computing 19 (1998) 1892-1917.
D. Levy (1998) [
gzipped file]Third-order 2D Central Schemes for Hyperbolic Conservation LawsINRIA School on Hyperbolic Systems Vol. I (1998) 489-504.
T. Katsaounis & D. Levy (1999) [
pdf file]A modified structured central scheme for 2D hyperbolic conservation lawsApplied Mathematics Letters 12 (1999) 89-96.
D. Levy, G. Puppo & G. Russo (2000) [
pdf file]A third order central WENO scheme for 2D conservation lawsApplied Numerical Mathematics 33 (2000) 415-421.
D. Levy, G. Puppo & G, Russo (2000) [
pdf file]Compact central WENO schemes for multidimensional conservation lawsSIAM Journal on Scientific Computing 22 (2000) 656-672.
A. Kurganov & G. Petrova (2001) [
pdf file]A third-order semi-discrete genuinely multidimensional central scheme for hyperbolic conservation laws and related problemsNumerische Mathematik 88 (2001) 683-729.
A. Kurganov, S. Noelle & G. Petrova (2000) [
pdf file]Semi-discrete central-upwind schemes for hyperbolic conservation laws and Hamilton-Jacobi equationsSIAM Journal on Scientific Computing 23 (2001) 707-740.
W. Rosenbaum, M. Rumpf & S. Noelle (2000) [
gzipped file]An adaptive staggered scheme for conservation laws"Hyperbolic Problems: Theory, Numerics, Applications"Proceedings of the 8th international conference held in Magdeburg, Feb. 2000
K.-A. Lie & S. Noelle (2003) [
pdf file]An improved quadrature rule for the flux computation in staggered central difference schemes in multi-dimensionsJournal of Scientific Computing 18 (2003) 69-81.
K.-A. Lie & S. Noelle (2000) [
gzipped file]A naive implementation of ACM in nonoscillatory central difference schemes for 2D Euler equationsProceedings of the 11th ECMI conference.
R. Liska & B. Wendroff (2002) [
pdf file]Comparison of several difference schemes on 1D and 2D test problems for the Euler equationsPreprint
D. Levy, G. Puppo & G. Russo (2002) [
pdf file]A forth order central WENO scheme for multi-dimensional hyperbolic systems of conservation lawsSIAM J. Scientific Computing 24 (2002) 480-506.
K.-A Lie, S. Noelle & Rosenabaum (2002) [
pdf file]On the resolution and stability of central difference schemesProceedings of the Third International Symposium on Finite Volumes for Complex ApplicationsPorquerolles, France, Hermes Penton Ltd, London (2002) 793-800.
X.-D. Liu & P. D. Lax (2003) [
pdf file]Positive schemes for solving multi-dimensional hyperbolic systems of conservation laws IIJ. Computational Physics 187 (2003) 428-440.
P. Arminjon & A. St-Cyr (2003) [
pdf file]Nessyahu朤admor-type central finite volume methods without爌redictor for 3D Cartesian and unstructured tetrahedral爂ridsApplied Numer. Math. 46 (2) (2003) 135-155.
L. Pareschi, G. Puppo & G. Russo (2004) [
pdf file]Central Runge-Kutta for conservation lawsPreprint
A. Kurganov & G. Petrova (2005) [
pdf file]Central-upwind schemes on triangular grids for hyperbolic systems of conservation lawsNumerical Methods for Partial Differential Equations 21 (2005), 536-552.
Central schemes on unstructured and overlapping grids
Back to TopP. Arminjon, M.-C. Viallon & A. Madarne (1997) [
html file]A finite volume extension of the Lax-Friedrichs and Nessyahu-Tadmor schemes for conservation laws on unstructured gridsInt'l J. Computational Fluid Dynamics 9(1) (1997), 1-22.
P. Arminjon & M.-C. Viallon (1999) [
pdf file]Convergence of a finite volume extension of the Nessyahu-Tadmor scheme on unstructured grids for a two-dimensional linear hyperbolic equations SIAM Journal on Numerical Analysis 36 (1999) 738-771.
B. Haasdonk, B. Kroner & D. Rohde (2001) [
pdf file]Convergence of a staggered Lax-Friedrichs scheme for nonlinear conservation laws on unstructured two-dimensional gridsNumerische Mathematik 88 (2001) 459-484.
M. Kuther (2001) [
pdf file]Error estimates for the staggered Lax-Friedrichs scheme on unstructured gridsSIAM Journal on Numerical Analysis 39 (2001) 1269-1301.
S. Karni, A. Kurganov & G. Petrova (2002) [
pdf file]A smoothness indicator for adaptive algorithms for hyperbolic systemsJ. of Computational Physics 178 (2003) 323-341.
M. Kuther and M. Ohlberger (2003) [
pdf file]Adaptive second-order central schemes on unstructured staggered gridsProceedings of the 9th international conference on "Hyperbolic Problems: Theory, Numerics, Applications"CalTech, Mar. 2002, (T. Hou & E. Tadmor eds.) Springer 2003, pp. 675-684.
P. Arminjon & A. St-Cyr (2003) [
pdf file]New space staggered and time interleaved 2nd order finite volume methodsProceedings of the 9th international conference on "Hyperbolic Problems: Theory, Numerics, Applications"CalTech, Mar. 2002, (T. Hou & E. Tadmor eds.) Springer 2003, pp. 295-304.
Yingjie Liu (2004) [
pdf file]Central Schemes on Overlapping CellsPreprint
Non-oscillatory central schemes for incompressible flows
Back to TopR. Kupferman & E. Tadmor (1997) [
pdf file]A fast high-resolution second-order central scheme for incompressible flowsProceedings of the National Academy of Sciences 94 (1997) 4848-4852.
D. Levy & E. Tadmor (1997) [
gzipped file]Non-oscillatory central schemes for the incompressible 2-D Euler equationsMathematics Research Letters 4 (1997) 1-20.
R. Kupferman (1998) [
pdf file]Simulation of viscoelastic fluids: Couette-Taylor FlowJournal of Computational Physics 147 (1998) 22-59.
R. Kupferman (1998) [
pdf file]A numerical study of the axisymmetric Couette-Taylor problem using a fast high-resolution second-order central schemeSIAM Journal on Scientific Computing 20 (1998), 858-877.
R. Kupferman & M. Denn (1999) [
pdf file]Simulation of the evolution of concentrated shear layers in a Maxwell fluid with a fast high-resolution finite-difference schemeJournal of Non-Newtonian Fluid Mechanics 84 (1999) 275-287.
R. Kupferman (2001) [
pdf file]A central-difference scheme for a pure streamfunction formulation of incompressible viscous flowSIAM Journal on Scientific Computing 23 (1) (2001) 1-18.
V. Naulin & A. Nielsen (2003) [
pdf file]Accuracy of spectral and finite difference schemes in 2D advection problemsSIAM Journal of Scientific Computing 25 (2003) 104-126.
R. Grauer & F. Spanier (2003) [
pdf file]A note on the use of central schemes for the incompressible Navier-Stokes flowsJournal of Computational Physics 192 (2003) 727-731.
Non-oscillatory central schemes -- Hamilton-Jacobi equations
Back to TopC.-T. Lin & E. Tadmor (1998) [
pdf file]L1-stability and error estimates for approximate Hamilton-Jacobi solutionsNumerische Mathematik 87 (2001) 701-735.
C.-T. Lin & E. Tadmor (2000) [
pdf file]High-resolution non-oscillatory central scheme for Hamilton-Jacobi equationsSIAM Journal on Scientific Computation 21 (2000) 2163-2186.
A. Kurganov & E. Tadmor (2000) [
pdf file]New high-resolution semi-discrete central schemes for Hamilton-Jacobi equationsJournal of Computational Physics 160 (2000) 720-742.
S. Bryson & D. Levy (2003) [
pdf file]High-order semi-discrete central-upwind schemes for multi-dimensional Hamilton-Jacobi equationsJournal of Computational Physics 189 (2003) 63-87.
S. Bryson & D. Levy (2003) [
pdf file]High-order schemes for multi-dimensional Hamilton-Jacobi equations"Hyperbolic Problems: Theory, Numerics, Applications", Proceedings of the 9th international conference held in CalTech, Mar. 2002, (T. Hou & E. Tadmor eds.) Springer 2003, pp. 387-396..
S. Bryson & D. Levy (2003) [
pdf file]Central schemes for multi-dimensional Hamilton-Jacobi equationsSIAM Journal on Scientific Computing 25, 2003, 769-791.
S. Bryson & D. Levy (2003) [
pdf file]High-order central WENO schemes for multi-dimensional Hamilton-Jacobi equationsSIAM Journal of Numerical Analysis 41, 2003, 1339-1369.
S. Bryson, A. Kurganov, D. Levy & G. Petrova (2004) [
pdf file]Semi-discrete central-upwind schemes with reduced dissipation for Hamilton-Jacobi equationsIMA J. Numerical Analysis 25, 2005, 113-138.
Applications of non-oscillatory central schemes to semi-conductors
Back to TopM. Trovato & P. Falsaperla (1998) [
pdf file]Full nonlinear closure for a hydrodynamical model of transport in siliconPhysical Review B-Condensed Matter 57 (1998) 4456-4471.
V. Romano & G. Russo (2000) [
gzipped file]Numerical solution for hydrodynamical models of semiconductorsMathematical Models & Methods in Applied Sciences 10 (2000) 1099-1120.
A. M. Anile, N. Nikiforakis & R. M. Pidatella (2000) [
pdf file] Assessment of a high resolution centered scheme for the solution of hydrodynamical semiconductor equationsSIAM Journal of Scientific Computing 22 (2000) 1533-1548.
A. M. Anile, V. Romano & G. Russo (2000) [
pdf file]Extended hydrodynamical model of carrier transport in semiconductorsSIAM Journal Applied Mathematics 61 (2000) 74-101.
A. M. Anile & V. Romano (2000)Hydrodynamical Modeling of Charge Carrier Transport in SemiconductorsMeccanica 35 (2000) 249-296.
V. Romano (2001) [
pdf file]2D simulation of a silicon MESFET with a nonparabolic hydrodynamical model based on the maximum entropy principleJournal of Computational Physics 176 (2001) 70-92.
V. Romano (2001) [
pdf file]Non-parabolic band hydrodynamical model of silicon semiconductors and simulation of electron devicesMathematical Methods in eth Applied Sciences 24 (2001) 439-471.
C. Gardner, A. Gelb & J. Hernandez (2002) [
gzipped file]A comparison of modern hyperbolic methods for semiconductor device simulation: NTK central schemes vs. CLAWPACKVLSI Design 15 (2002) 721-728.
Applications to Sedimentation, Flocculations and related models
Back to TopR. Burger & F. Concha (1998) [
pdf file]Mathematical model and numerical simulation of the setting of flocculated suspensionsInternational Journal of Multiphase Flow 24 (1998) 1005-1023.
E. B. Pitman (1998) [
pdf file]Forces on bins: The effect of random frictionPhysical Review E 57 (1998) 3170-3175.
R. Burger, F. Concha, K. K. Fjelde, & K. H. Karlsen (2000) [
pdf file]Numerical simulation of the setlling of polydisprese suspensions of spheresPowder Technology 113 (2000) 30-54.
R. B黵ger, S. Evje, K. H. Karlsen & K.-A. Lie (2000) [
pdf file]Numerical methods for the simulation of the settling of flocculated suspensionsChemical Engineering Journal 80 (2000) 91-104.
R. Burger, K. -K Fjelde, K. Hofler, & K. H. Karlsen (2000) [
pdf file]Central difference solutions of the kinematic model of settling of polydispersesuspensions and three-dimensional particle-scale simulationsJournal of Engineering Mathematics 41 (2001) 167-187.
B. Xue & Y. Sun (2003) [
pdf file]Modeling of sedimentation of polydisperese spherical beads with a broad size distributionChemical Engineering Science 58 (2003) 1531-1543.
S. Berres & R. Bürger (2003) [
pdf file]On gravity and centrifugal settling of polydisperse suspensions forming compressible sedimentsInt'l J. Solids & Structures 40 (2003), 4965-4987.
S. Berres, R. Bürger, K. H. Karlsen & E. M. Tory (2003) [
pdf file]Strongly degenerate parabolic-hyperbolic systems modeling polydisperse sedimentation with compressionSIAM J. Applied Mathematics 64 (2003), 41-80.
S. Berres, R. Bürger & K. H. Karlsen (2004) [
pdf file]Central schemes and systems of conservation laws with discontinuous coefficients modeling gravity separation of polydisperse suspensionsJ. Comp. Appl. Math. 164-165 (2004) 53-80
S. Berres, R. Bürger & E. M. Tory (2004) [
pdf file]Mathematical model and numerical simulation of the liquid fluidization of polydisperse solid particle mixturesComput. Visual Sci. 6 (2004) 67-74.
Non-oscillatory central schemes -- applications to > Multi-component problems
Back to TopB. Engquist & O. Runborg (1996) [
pdf file]Multiphase computations in geometrical opticsJournal of Computational and Applied Mathematics 74 (1996) 175-192.
R. Fazio & G. Russo (2000) [
gzipped file]A Lagrangian central scheme for multi-fluid flows"Hyperbolic Problems: Theory, Numerics, Applications", Proceedings of the 8th Int'l conference held in Magdeburg, Feb. 2000
L. Gosse (2002) [
gzipped file]Using K-branch entropy solutions for multivalued geometric optics computationsPreprint
S. Karni, E. Kirr, A. Kurganov & G. Petrova (2003) [
pdf file]Compressible two-phase flows by central and upwind schemesMathematical Modeling and Numerical Analysis 38 (3) (2004) 477-494.
Non-oscillatory central schemes -- applications to > Relaxation problems and stiff source terms
Back to TopF. Bereux & L. Sainsaulieu (1997) [
pdf file]A Roe-type Riemann solver for hyperbolic systems with relaxation based on time-dependent wave-decompositionNumerische Mathematik 77 (1997) 143-185.
S. F. Liotta, V. Romano & G. Russo (2000) [
pdf file]Central schemes for balance laws of relaxation typeSIAM Journal on Numerical Analysis 38 (2000) 1337-1356.
L. Pareschi (2001) [
pdf file]Central differencing based numerical schemes for hyperbolic conservation laws with relaxation termsSIAM Journal Numerical Analysis 39 (2001) 1395-1417.
C. Arvanitis, T. Katsaounis & C. Makridakis (2001) [
pdf file]Adaptive finite element relaxation schemes for hyperbolic conservation lawsMathematical Modeling and Numerical Analysis 35 (1) (2001) 17-33.
S. Jin, L. Pareschi & M. Slemrod (2002) [
gzipped file]A relaxation scheme for solving the Boltzmann equation based on the Chapman-Enskog expansionActa Mathematicas Applicatae Sinica (English Series) 18, No.1, (2002).
A. Kurganov (2002) [
pdf file]An accurate deterministic projection method for hyerbolic systems with stif source term"Hyperbolic Problems: Theory, Numerics, Applications", Proceedings of the 9th international conference held in CalTech, Mar. 2002, (T. Hou & E. Tadmor eds.) Springer 2003, pp. 665-674.
Non-oscillatory central schemes -- applications to > Extended thermodynamics
Back to TopM. Torrilhon (2000) [
pdf file]Characteristic waves and dissipation in the 13-moment-caseContinuum Mech. Thermodynamics 12 (2000) 289-301.
Non-oscillatory central schemes -- applications to > Balance laws
Back to TopS. F. Liotta, V. Romano & G. Russo (1998) [
gzipped file]Central schemes for systems of balance laws"Hyperbolic Problems: Theory, Numerics, Applications", Proceedings of the 7th Int'l conference held in Zurich, Feb. 1998 (M. Fey and R. Jeltsch, eds.), Int'l Series on Numerical Mathematics, Birkhauser, Vol. 130, 1999, 651-660
G. Russo (2002) [
pdf file]Central schemes and systems of balance lawsin "Hyperbolic Partial Differential Equations, Theory, Numerics and Applications", (A. Meister and I. Struckmeier,eds.) Vieweg, Wiesbaden (D), 2002.
A. Kurganov & D. Levy (2002) [
pdf file]Central-Upwind Schemes for the Saint-Venant SystemMathematical Modeling and Numerical Analysis 36 (2002) 397-425.
N. Crnjaric-Zic, S. Vukovic & L. Sopta (2004) [
pdf file]Balanced finite volume WENO and central WENO schemes for the shallow water and the open-channel flow equationsJournal of Computational Physics 200 (2004) 512-548.
S. Bryson, A. Kosovichev & D. Levy (2005) [
pdf file]High-order shock-capturing methods for modeling dynamics of the solar atmosphereNonlinearity 201 (2005) 1-26.
A. Chertok & A. Kurganov (2004) [
pdf file]On a Hybrid Finite-Volume-Particle MethodMathematical Modeling and Numerical Analysis 38(6) (2004) 1071-1091.
Non-oscillatory central schemes -- applications to > Saturating dissipation
Back to TopA. Kurganov & P. Rosenau (1997) [
pdf file]Effects of a saturating dissipation in Burgers-type equationsCommunications on Pure and Applied Math. L (1997) 753-771.
A. Kurganov, D. Levy & P. Rosenau (1998) [
pdf file]On Burgers-type equations with nonmonotonic dissipative fluxesCommunications on Pure & Applied Mathematics LI (1998) 443-473.
J. Goodman, A. Kurganov & P. Rosenau (1999) [
pdf file]Breakdown in Burgers-type equations with saturating dissipation fluxesNonlinearity 12 (1999) 247-268.
J. Otero, L. A. Dontcheva, H. Johnston, R. A. Worthing, A. Kurganov, G. Petrova & C. Doering (2004) [
pdf file]High Raleigh Number Convection in a Fluid Saturated Porous LayerJournal of Fluid Mechanics 500 (2004), 263-281.
Non-oscillatory central schemes -- applications to > Homogenization and Multiscale
Back to TopE. Tadmor & T. Tassa (1997) [
pdf file]On the homogenization of oscillatory solutions to nonlinear convection-diffusion equationsAdvances in Mathematical Sciences and Applications 7(1) (1997) 93-117.
X. Li & W. E (2004) [
pdf file]Multiscale modeling of the dynamics of solids at finite temperatureJ. Mech. Phys. solids(53) 2004, 1650-1685.
Non-oscillatory central schemes -- applications to > Discrete kinetic models
Back to TopE. Gabetta, L. Pareschi & M. Ronconi (2000) [
gzipped file]Central schemes for hydrodynamical limits of discrete-velocity kinetic modelsTransport Theory and Statistical Physics 29 (2000) 465-477.
A. Kurganov (2002) [
pdf file]Semi-discrete central schemes for balance laws. Application to the Broadwell modelProceedings of the Third International Symposium on Finite Volumes for Complex Applications
Non-oscillatory central schemes -- applications to > MHD
Back to TopC.C. Wu & T. Chang (2001) [
pdf file]Further study of the dynamics of two-dimensional MHD coherent structures -- a large-scale simulationJournal of Atmospheric and Solar-Terrestrial Physics 63 (2001) 1447-1453.
K. Germaschewski, A. Bhattacharjee, T. Linde, R. Rosner, A. Siegel, D. Keyes & F. Dobrian (2003) [
pdf file]The magnetic reconnection code: framework and application
SciDAC-TOPS,
CMRS poster.
M. Torrilhon (2003) [
pdf file]Non-uniform convergence of finite volume schemes for Riemann problems of ideal magnetohydrodynamicsJournal of Computational Physics 192(1) (2003) 73-94.
J. Kleimann, A. Kopp, H. Fichtner, R. Grauer, & K. Germaschewski (2004) [
pdf file]Thre-dimensional MHD high-resolution computations with CWENO employing adaptive mesh refinmentComput. Physics Communication 158 (2004) 47-56.
J. Balbas, E. Tadmor, & C.-C. Wu?2004) [
pdf file]Non-oscillatory central schemes for one- and two-dimensional MHD equationsJournal of Computational Physics 201 (2004) 261-285.
P. Arminjon & R. Touma?2004) [
pdf file]Central finite volume methods with constrained transport divergence treatment for ideal MHDJournal of Computational Physics (2004)
J. Balbas & E. Tadmor (2005) [
pdf file]Non-oscillatory central schemes for one- and two-dimensional MHD equations. II: High-order semi-discrete schemesPreprint (2005)
Non-oscillatory central schemes -- applications to > The p-system
Back to TopF. Hoch & M. Rascle (1999) [
pdf file]A numerical study of a pathological example of p-systemSIAM Journal of Numerical Analysis 36 (1999) 1588-1603.
Non-oscillatory central schemes -- applications to > Riemann problems
Back to TopA. Kurganov & E. Tadmor (2000) [
pdf file]Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solversNumerical Methods for Partial Differential Equations 18 (2002) 548-608.
Non-oscillatory central schemes -- applications to > Granular Avalanches
Back to TopY.C. Tai, S. Noelle, J.M. N.T. Gray & K. Hutter (2001) [
pdf file]Shock-capturing and front-tracking methods for granular avalanchesJournal of Computational Physics 175 (2001) 269-301.
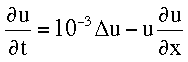
 )) this means that for some instances the Jacobian may become zero or almost zero.
)) this means that for some instances the Jacobian may become zero or almost zero.